2. Charges in the UMIE Model
First, consider the structure of the Super-Universe and the charges in them
| [7] | Petro O. Kondratenko. Model of the Creation and Evolution of the Universe with Minimal Initial Entropy. Fundamental Interactions in the Universe / LAMBERT Academic Publishing. - 2017. – 130 p. https://kondratenko.com.ua |
| [8] | Petro O. Kondratenko. The birth and evolution of the Universe with minimal initial entropy // International Journal of Physics and Astronomy. December 2015, Vol. 3, No. 2, pp. 1-21. Published by American Research Institute for Policy Development https://doi.org/10.15640/ijpa.v3n2a1 |
[7, 8]
.
The UMIE model was created based on the Laws of Unity and Similarity in the Universe and fully meets the requirements of the laws of physics
| [7] | Petro O. Kondratenko. Model of the Creation and Evolution of the Universe with Minimal Initial Entropy. Fundamental Interactions in the Universe / LAMBERT Academic Publishing. - 2017. – 130 p. https://kondratenko.com.ua |
| [8] | Petro O. Kondratenko. The birth and evolution of the Universe with minimal initial entropy // International Journal of Physics and Astronomy. December 2015, Vol. 3, No. 2, pp. 1-21. Published by American Research Institute for Policy Development https://doi.org/10.15640/ijpa.v3n2a1 |
[7, 8]
. According to the UMIE model, our Universe is part of the Super-Universe, represented by a stratified space of four layers. In the created Super-Universe, the first layer is depicted as zero-dimensional space. The second layer is one-dimensional space, the third is two-dimensional, and the fourth is our three-dimensional space. There is an information interaction between adjacent layers through one delocalized point.
At the beginning of the creation of the Super-Universe, each layer is represented by a space with collapsed coordinates of fundamental dimensions. The first layer has 12 collapsed spatial coordinates and time and information coordinates. The second layer has three collapsed spatial coordinates, one of which eventually unfolds as a brane of two-dimensional space (a circle whose radius increases with the speed of light). The third layer has three collapsed spatial coordinates, two of which eventually unfold as a brane of three-dimensional space (a sphere whose radius increases with the speed of light). The fourth layer has 6 spatial coordinates, three of which are revealed as a brane of four-dimensional space. At the same time, the radius of the four-dimensional sphere increases with the speed of light. Time and information coordinates are common to all layers of the layered space.
12 collapsed spatial coordinates of zero-dimensional space cover all spatial coordinates of stratified space, which makes it possible to interact between processes occurring in zero-dimensional space with processes occurring in other spaces. In this way, individual layers of stratified space are closed spaces.
A Scalar Field (SF) enters the zero-dimensional space at a constant speed
. SF carries the program (
universal code) for creating the Super-Universe. This Field initially fills only one-dimensional space before reaching a constant density of matter in this space. The SF introduction rate should be 3 times higher than required to maintain a constant density of matter in a one-dimensional, constantly expanding space. Then SF fills the two-dimensional space, and, finally, starting from
=3·10
-5 s, our Universe begins to fill. This mechanism of filling spaces prevents their transformation into black holes.
The calculation shows that Planck particles are born in one-dimensional space. These particles are dyons, carriers of electric and magnetic charges. The existence of dyons in one-dimensional space is facilitated by magnetic monopoles having a one-dimensional topological charge
. Quarks known from physics are born in two-dimensional space. The information connection between spaces leads to the fact that in two-dimensional space, particles rigidly connected to baryons of three-dimensional space appear, and in one-dimensional space, particles rigidly connected to quarks are born. Such a connection is due to spatial metamorphosis
.
By studying the internal structure of nucleons or bosons in three-dimensional space, we experience information about the spatial metamorphosis of quarks associated with a given nucleon or boson. Since a colorless quark structure is related to the nucleon or boson, the color charge is not transferred into three-dimensional space, while the electric charge and spin are transferred. Similarly, the magnetic charge of dyons is not transferred to quarks but forms their spins. In addition, the corresponding spatial metamorphosis forms the colored charges of quarks. Therefore, part of the quantum numbers is lost when moving to a higher-dimensional space. Thus, the magnetic charge of Planck particles determines the creation of spin in quarks and particles of the Universe. Therefore, the color charge of quarks disappears when moving to three-dimensional space.
Since there is only informational interaction between spaces, we can only see the quark mass's practical value, not its actual value, in experimental studies.
The dimensionality of the space determines the value of the minimum electric charge of the particle. Therefore, quarks, being localized in two-dimensional space, have a charge q2 = ±e/3 and ±2e/3, and particles of one-dimensional space have a charge q1 = ±q2/2 = ±e/6. Thus, we introduced magnetic, electric, and color charges in one-dimensional and two-dimensional spaces because they cause interactions in the respective spaces.
Since all the coordinates of the zero-dimensional space are enclosed in small-radius circles, the SF wave must be circularly polarized. This, in turn, will cause all created matter in the Universe to have a rotational moment. From the atom to the galaxy, everything revolves.
During the time
, the brane radius of the four-dimensional space will reach 9 km. The newborn three-dimensional space will initially be filled only with vacuum particles
and zero fluctuations of physical fields. The entry of a large flow of SF energy will lead to the excitation of vacuum particles to a free state and the birth of other material particles in the vicinity of the particles, which can only be neutrons or neutron complexes
. Subsequently, bineutrons are born in the area of nucleons, increasing the mass of atomic nuclei. The flow of radiation processes in heavy nuclei leads to the birth of many secondary atomic nuclei and an increase in the mass and temperature of newborn stars and planets.
Let's pay attention to one more fact. The analysis shows that only those large systems organized according to the hierarchical principle can be sustainable. All other systems in the process of evolution must cease to exist due to their instability
. Therefore, the result of the evolution of any sizeable natural system is the formation of its hierarchical structure
.
Then, it turned out that each structure corresponds to a separate physical interaction. However, an arbitrary hierarchical system should have 7 levels
. This is also the hierarchical structure of our Universe (
table 1).
Table 1. Hierarchical structure of the Universe.
HL | Substance | Interaction | Reaction |
1 | Elementary particles | Weak | Particle decay and lepton scattering on baryons |
2 | Atomic nuclei | Strong | Interaction between baryons |
3 | Atoms, molecules, molecular systems, plasma | Electromagnetic | Interaction between electric charges |
4 | Planetary systems | Gravitational І | Interaction between gravitating bodies within the planetary system |
5 | Star systems | Gravitational ІІ | Interaction between stars within the galaxy |
6 | Cluster of galaxies | Gravitational ІІІ | Interaction between galaxies (cellular structure of the Universe) |
7 | Metagalaxy | Gravitational ІV | Interaction between galaxy clusters |
8 | God of the system | | |
It follows from
Table 1 that in addition to the known interactions, there must also be other interactions that manifest themselves on a large scale
. At the same time, 7 principles describing hierarchical structures are described in
. The first principle is the Law of Unity within the element of the hierarchical level (HL).
Interaction for a separate element of HL ensures temporal unity concerning all other aspects of the same IR - interaction between them. Temporal unity means that within the time limit Δt = h/mc2, the unity signal will cover the characteristic (smallest, with mass m) HL element. This fact causes different properties of gravitational fields at different HLs.
Experience shows that the transformation of a star into a black hole does not lead to the disappearance of the gravitational attraction of stars to the black hole. It exists and ensures that matter from near space is captured by a black hole, including stars and other black holes that have come close enough to the black hole.
We have already discussed similar phenomena in the article
| [13] | Petro O. Kondratenko. Creation and Evolution of the Galaxy in the Universe Model with Initial Minimum Entropy // International Journal of Advanced Research in Physical Science (IJARPS). - Volume 6, Issue 6(6), 2019, pp. 1-11. URL: https://www.arcjournals.org/pdfs/ijarps/v6-i6/1.pdf |
[13]
, where it was shown that galactic arms could form only due to the merger of black holes. At the same time, the exit of matter beyond the boundaries of black holes could be ensured only by a multi-dimensional SF
.
Thus, only the SF and the gravitational waves generated by the SF, manifesting their multidimensionality, can go beyond the black hole.
Using its multidimensionality and the presence of information interaction between the layers of stratified space provided by SF and occurs through a delocalized point, SF "knows" the coordinates of all masses in the Universe
. Therefore, it can always organize interaction between massive bodies (planets, stars) or massive systems of bodies (galaxies or clusters of galaxies). Not only SF but also the gravitational waves generated by it must have a dimension that exceeds the dimension of our Universe. In contrast to the gravitational interaction, the electromagnetic interaction exists only within the limits of one space. It, therefore, cannot be manifested at great distances (even within the boundaries of the Solar System).
The multidimensionality of SF and gravitational waves will be responsible for the extremely weak gravitational interaction between bodies. Gravitational interaction, considering the Universe's hierarchical structure, is considered by the author in the article
| [14] | Petro O. Kondratenko. Universe hierarchy and gravitational interaction // International Journal of Advanced Research in Physical Science (IJARPS) Volume 10, Issue 9, 2023, PP 1-9. ISSN (Online) 2349-7882. https://doi.org/10.20431/2349-7882.1009001 |
[14]
.
According to the hierarchical structure of the Universe, the SF, in which the hierarchical structure is programmed, immediately forms the seeds of stars, galaxies, and clusters of galaxies. The information dimension programs this structure. The expansion of space and the increase in the mass of stars led to the creation of the Universe that we can see now.
The proposed mechanism of the evolution of the Universe will lead to the birth of heavy atomic nuclei in the first moments after its creation.
Now, let's return to the charges.
It is clear that the magnetic and electric charges of one-dimensional space are accurate charges that organize the interaction between them with the help of virtual bosons.
Spin in two-dimensional space is conserved, but it is a number because there is no corresponding charge. However, having a dipole moment, the spin-spin interaction is realized through a magnetic field.
The color charge of quarks interacts with them with the help of gluons (bosons). However, the theory is incomplete in this case since there is no calibration field. Therefore, there is a lack of understanding of how virtual gluons know in which direction and when to fly to ensure color interactions. Physicists have no understanding of why gluons, being represented by two colorless (white) combinations
are carriers of interaction, and the third cannot be a carrier of color interaction between quarks. The reason for the lack of interaction in the case of a completely symmetric combination concerning colors is easy to understand using the wave function of three interacting atoms (for example, iodine). At the same time, the fully symmetric combination gives the minimum energy of the molecule, the antisymmetric one (g3) corresponds to the absence of binding energy between atoms and, therefore, leaves the energy of the parts unchanged, and the third (g8) is loosening and characterizes the increased energy of the state.
For binding to occur, the energy of the quark plus the energy of the virtual gluon must exceed the energy of the quark. It should be assumed that in the case of a fully symmetric wave function of a gluon, the total energy does not differ from the energy of a quark, i.e., a fully symmetric combination corresponds to an elementary vacuum particle. In this case, a fully symmetric gluon will not be able to provide binding between quarks. The lack of interaction will not be in the color combination but in the energy of the quark plus the virtual gluon.
Now consider charges in three-dimensional space.
2.1. Weak Interaction Charges
The appearance of neutrons in three-dimensional space is accompanied by virtual W
±(Z
о) - bosons responsible for the weak interaction
| [15] | R. Feynman. QED - a strange theory of light and substance. - Princeton University Press. 1988. - 158 pp. ISBN 9780691083889. |
[15]
. Since a change of neutrons and quarks accompanies such an interaction, such bosons must be located in two-dimensional and three-dimensional spaces connected through spatial metamorphosis.
The radius of the weak interaction is R≈ 2·10
-18 m
| [16] | L. B. Okun. Weak interaction // Physical encyclopedia / edited A. M. Prokhorov. — Moscow: Soviet Encyclopedia, 1994. — V. 4. — P. 552–556. — 704 pp. |
[16]
(the Compton radius for the
W - boson is equal to 1.54·10
-17 m, and for the
Zо - boson 1.36·10
-17 m), i.e. significantly smaller than the size of a neutron. So these bosons do not go beyond the boundaries of the nucleon during their lifetime. Therefore, a neutron decays in 881 s
. Therefore, the neutrino interacts weakly with matter.
Currently, the scheme of the weak interaction is adopted, according to which the d-quark emits a W
–- boson, turning into a u-quark. In turn, the virtual W
–- boson decays into a pair of real leptons: an electron and an antineutrino
| [15] | R. Feynman. QED - a strange theory of light and substance. - Princeton University Press. 1988. - 158 pp. ISBN 9780691083889. |
[15]
. So, we have the first contradiction of the known scheme of weak interaction. In addition, it is not clear why nature needs the Z
o- boson. In this regard, we will consider the weak interaction from the standpoint of the UMIE model.
It is necessary to understand that during the life of a virtual particle, it can transform into another virtual particle with the birth of quarks in two-dimensional space or leptons in three-dimensional space. The fact that, according to calculations, the free Zo- boson is more massive (91.2 GeV) than the W±- boson (80.4 GeV) does not prevent such processes since both bosons remain virtual (associated with quarks or neutrons). Moreover, the released energy during such a transformation (the energy level of a more massive virtual particle must lie much deeper) should provide the possibility of the birth of a pair of free leptons, mainly an electron and an electron antineutrino.
Thus, the proposed scheme shows why the Zo-boson is needed.
Since the instability is detected only by the neutron, it must be assumed that the d-quark can emit weakly interacting bosons only in the presence of a pair of quarks (ud). The proton also includes a pair of quarks (ud), but it is unable to activate the u-quark boson emission. Nevertheless, the β+- activity of nuclei is known, from which it follows that the u-quark can be activated by additional interaction with surrounding protons (β+- activity exists only with an excess of protons).
It is necessary to understand that the W
±(Z
о)-boson and the lepton or quark have mass, so they have a localized SF resulting from a weak interaction. When a lepton flies past a neutron so that their SFs overlap, it causes the birth of a W
±- boson (the nuclear time is much longer than the lifetime and interaction time of a lepton with a W
±- boson) and at a certain distance between the lepton and the boson
| [16] | L. B. Okun. Weak interaction // Physical encyclopedia / edited A. M. Prokhorov. — Moscow: Soviet Encyclopedia, 1994. — V. 4. — P. 552–556. — 704 pp. |
[16]
a weak interaction occurs between them with lepton conversion or scattering. At the same time, the electron or neutrino does not emit the W
±- boson. Therefore, neutrino scattering on an electron is impossible.
In the two-dimensional world, transforming a W
–– boson into a Z
o– boson is accompanied by the birth in a virtual state of a pair of quarks with a total electric charge of -1 and a total spin of s = 0. This is the same pair of quarks that forms a π
–- meson. Since the density of quark matter is high
| [8] | Petro O. Kondratenko. The birth and evolution of the Universe with minimal initial entropy // International Journal of Physics and Astronomy. December 2015, Vol. 3, No. 2, pp. 1-21. Published by American Research Institute for Policy Development https://doi.org/10.15640/ijpa.v3n2a1 |
[8]
, this causes interaction between the virtual particle and the real u. When this pair is annihilated, the energy needed to release the d-quark will be released. This corresponds to the decay of a neutron into a proton and lepton.
In the given description of the weak interaction, it should be remembered that a boson in the Universe must correspond to a boson in the two-dimensional world due to spatial metamorphosis
.
Thus, we learned that only leptons are involved in weak interaction processes in three-dimensional space. They can scatter on nucleons, cause a transformation into a lepton-neutrino and neutron-proton pair, and cause a neutron to decay without changing the baryon charge with the formation of a lepton pair with a total zero lepton charge. From this, we draw an unambiguous conclusion: the lepton charge exists and provides a weak interaction in the three-dimensional world. The controlling field in this case is the SF, and the interaction boson is the W±(Zо)- boson, although another particle emits it under the action of the SF.
2.2. Charges of the Strong Interaction
The Japanese physicist Hideki Yukawa first described strong intranuclear interaction in 1935 using exchangeable particles — mesons. A modern description of the strong interaction is given by quantum chromodynamics, which is included in the Standard Model, which is the sum of contemporary ideas about the structure of the microcosm.
According to the Yukawa model, the strong interaction in the Universe is manifested because one nucleon emits a π-meson, and the second one absorbs it during the time t ~10-23 s. At the same time, it is not known what is the calibration field of the strong interaction.
According to the Standard Model, it is necessary to consider three quarks to describe the properties of a hadron and two quarks to describe a meson. In both cases, the combination of quarks must be colorless. So, currently, within the framework of the Standard Model, a connection between quarks and hadrons has been found.
Next, we will continue by describing the strong interaction within the framework of the UMIE model. This model includes an understanding of the nature and structure of the physical vacuum (PV): upon annihilation of the particle-antiparticle pair, they are not eliminated but combined into a system called the elementary vacuum particle (EVP). In EVP, in the unexcited state of our laboratory space, all quantum numbers are equal to zero. According to
, the basis of the physical vacuum is the proton-antiproton (p
+p
–) vacuum. The EVP concentration in this type of vacuum equals 1.54541·10
39 cm
-3, while the EVP concentration of the electron-positron vacuum equals 1.73009·10
29 cm, which is 10 orders of magnitude lower. In addition, EVPs form all stable particles of two-dimensional and three-dimensional spaces. The author's work
describes the properties of SF, which explain the cause of the appearance of vacuum particles. Other known interactions cannot create vacuum particles, which are absent in the Standard Model.
The charges of quarks for a proton (uud) are combined into +1 (in units of elementary charge), and for a neutron (udd) - into 0. At the same time, the total color charge of quarks is always white; that is, the color charge is not transferred to the Universe in the process of spatial metamorphosis.
Gluons, quanta of the strong interaction field, hold quarks together.
Quarks have a kind of charge called "color." At any moment, a quark can be in one of three states or colors - red, blue, or green (r, b, g). When a gluon is absorbed or emitted, the color of the quark can change, for example:
A gluon has spin 1, like a photon, has 2 spin states, is electroneutral, and has a color charge
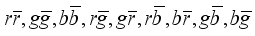
. The charges of gluons, which are in the field of reduced symmetry, are given here. The symmetry of the free gluon is described in terms of the SU (3) group.
The exchange of such gluons between quarks will describe the interquark interaction. However, in quantum chromodynamics and quantum mechanics, the interaction is described using wave functions, the symmetry of which must correspond to the symmetry of the local space. Therefore, linear combinations of wave functions are first found to satisfy the condition of the problem.
The existence of quarks thoroughly explains the presence of a magnetic moment in a proton (2.79275·μp) and a neutron (-1.93·μp).
The strong interaction between hadrons is described using the exchange of pions, the structure of which is represented by a quark and an antiquark, which carry color and anticolor. So, pions are colorless particles with zero spin (bosons). Pions are unstable particles. The lifetime of π+ and π- - mesons is 2.60·10-8 s, and the π0 meson is 0.85·10-16 s.
Based on the uncertainty ratio,
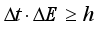 (2)
(2) we will find the distance to which the virtual boson will move during the time Δt
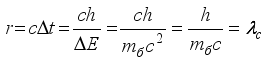 (3)
(3) This distance will be the radius of particle interaction. If the boson is a pion (mπ± = 273 me), then r = 8.9·10-15 m.
Therefore, the strong interaction between nucleons is manifested because one nucleon emits a virtual π-meson (pion), and the other absorbs it. The birth of pions in the Standard Model is not described. It is simply assumed that all processes occur within the framework of the uncertainty ratio.
Now let's look at the internucleon interaction at the quark level.
In the field of the proton, a virtual pion π+ is born, which is transferred to the neutron, turning it into a proton due to the destruction of the d quark of the neutron with the antiquark of the pion. At the same time, the u-quark remaining from the pion is part of the newly formed proton. Since the pion is in a virtual state, the release of energy does not accompany such annihilation; there is no γ-quantum emission.
As for the criticism of the Standard Model of the strong interaction, the first thing that comes to mind is the inconsistency of the exchange interaction model with the potentials that describe the strong interaction between hadrons. The potentials found by theorists do not in any way follow from the exchange processes in the hadron. It seems that gluons somehow know in which direction they should radiate and what color and spin characteristics they should have. Where does this knowledge come from if nothing exists between hadrons except gluons? The exchange interaction in the described model should be chaotic rather than strictly deterministic. So what directs the virtual gluons, ensuring the deterministic interaction between hadrons?
The Law of Similarity operates in nature. Therefore, the interaction between quarks using bosons (gluons) can be considered an example of the interaction between atoms utilizing a pair of electrons (also bosons) in the singlet state. At the same time, the guiding force for the movement of these bosons will be the electromagnetic field. Therefore, the movement of gluons must be provided by an appropriate field.
Let's change the scheme of the strong interaction so that it is consistent with the new model of the Universe's birth as a Super-Universe component.
Quarks and gluons are in two-dimensional space, and nucleons and pions are in three-dimensional space. We used this approach when considering a weak interaction
| [18] | Petro O. Kondratenko. Quarks and Leptons in the Model of the Universe with a Minimum Initial Entropy. // International Journal of Physics and Astronomy. December 2015, Vol. 3, No. 2, pp. 51-69. Published by American Research Institute for Policy Development. URL: http://dx.doi.org/10.15640/ijpa.v3n2a4 |
[18]
. Now, we will use it to describe the details of the strong interaction between quarks and hadrons.
Both quarks and nucleons are simultaneously SF carriers
.
Cyclic transfer of gluons in a triplet of quarks [½d(g) + ½u(r) + -½u(b)] in the case of a proton or a triplet [½d(g)+ -½d(r)+ ½u(b)] in the case of a neutron provides strong interaction. At the same time, a gluon with a spin projection of 1 is transferred to a quark whose spin is equal to (-½), and vice versa, if the gluon spin projection is opposite. In addition, the color composition of the gluon must correspond to the colors of the quarks between which it is transferred. This exhausts the condition for an intense color interaction between quarks.
Strong colorless interaction between nucleons co-occurs in two-dimensional and three-dimensional spaces. At the same time, in the Universe, we have the standard Yukawa scheme of transferring a virtual pion between nucleons. Virtual pions in two-dimensional space are born by SF quark energy of vacuum particles [
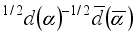
] or [
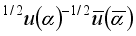
], where α = r, g, b. Therefore, the power of SF quarks will be generated from vacuum particles under conditions of reduced symmetry, with only a neutral quark-antiquark pair corresponding to a neutral pion in the Universe. If this pair was born in the triplet of quarks, which are the constituents of a neutron, then it should have a quark structure
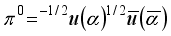
and the constituents of a proton -
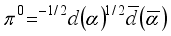
.
In all cases, colorless virtual pairs of quarks and neutral pions (themselves particles and antiparticles), consisting of a quark and an antiquark in a singlet state, are first formed from vacuum particles. At the same time, the energy of the system of quarks that make up a nucleon decreases by the amount of excitation of a virtual neutral pion. This virtual pair can interact with the quark triplet that created it (in both spaces) or return to the vacuum. In the latter case, the SF nucleon energy is restored.
A virtual pair (pion π
o) can move to another nucleon, causing a solid colorless interaction between nucleons. The movement of a virtual pion between nucleons causes a movement in the opposite direction of the SF energy, which causes the birth of a virtual pair. The movement of the pion resembles a ship along a narrow channel between two small bodies of water. The ship displaces part of the water from the reservoir in which it is located. Moving the ship into the second body of water causes water to flow from the second body of water into the first body of water. After moving, the virtual pawn will return to the vacuum. At the same time, the energy of the nucleon field will increase to the standard state. The overlapping of the SF of interacting nucleons and the reduction of the total energy of the SF will determine both the direction of movement of the virtual boson and the interaction between nucleons (
Figure 1). Therefore, the role of SF in the interaction between nucleons with the participation of bosons is similar to the role of the electromagnetic field in the interaction between atoms with the participation of a pair of electrons in the singlet state.
Figure 1. Overlap of SF of interacting nucleons in the triplet state.
After the birth of a virtual pion in the SF neutron, an exchange of quarks is possible without changing colors.
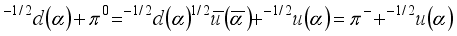 (4)
(4) At the same time, π– flies out of the neutron, and the neutron turns into a proton. The reaction proceeds similarly in the SF of a proton. At the same time, quarks are exchanged
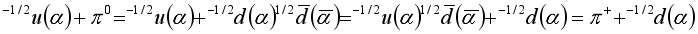 (5)
(5) Therefore, π+ flies out of the proton, and the proton turns into a neutron. It can be expected that the exchange of quarks with the constituents of the virtual neutral pion will require additional energy from the SF quarks. The movement of the charged pion to the partner nucleon requires the reverse reaction of the transformation of the charged pion into a neutral pion and relaxation of the latter to the vacuum state. At the same time, in all transformation processes, the antiquark that enters the virtual particle remains in the virtual particle. The birth process of a virtual particle and its relaxation to a vacuum state resembles an oscillatory motion. Therefore, this process is constantly occurring, providing a constant value of the interaction between quarks and between nucleons. There is an additional possibility for the manifestation of intense interaction between nucleons. In the three-dimensional world, the pion π+ is the antiparticle to π–. Therefore, the energy of the total SF of a neutron and a proton can give birth to a virtual pair (π–π+). In the proton's electrostatic field, this virtual pair is polarized, after which π– interacts with the proton, and π+ interacts with the neutron:
The last process in reactions (6) is the return of neutral pions to the vacuum state. In two-dimensional space, the formation of a virtual pair (π
–π
+) means the simultaneous formation of quark virtual pairs
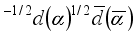
and
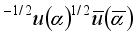
. In the field of a group of quarks that make up a proton and a neutron, the polarization of these pairs and the exchange of quarks in their structures take place:
what corresponds to the formation of pions π+ and π– in the Universe.
It is important to note that when considering the interaction of two protons or two neutrons, reaction (7) is impossible. Therefore, interaction between the same nucleons is possible only due to the exchange of neutral pions. And this, in turn, leads to the impossibility of forming a stable helium-2 nucleus, which would consist of only two protons (biproton).
According to literature data, the interaction energy between protons in a biproton is -0.5 MeV. Since the power of electrostatic repulsion is equal to ≈1 MeV, the share of the binding energy due to the transfer of a neutral pion is 0.5 MeV
. The same binding energy must exist in the bineutron. However, the bineutron is unstable due to the occurrence of the weak interaction reaction.
On the other hand, in a deuteron, the interaction energy is 2.22457 MeV
, as the transfer of a pair of charged pions causes it. Thus, since there is a strong interaction between baryons, we conclude that there is a baryon charge.
2.3. Charges of Electromagnetic Interaction
The energy of the electrostatic interaction between an electron and a proton, depending on the distance between them, is
Let's imagine that this interaction occurs by transferring a virtual photon between charges. In this case, a standing electromagnetic wave will be established between the charges, and the length of this wave will be equal to twice the distance between the charges. You can calculate the energy of the photon and compare it with the energy of the Coulomb interaction.
,
i.e., the photon energy is 3 orders of magnitude greater than the Coulomb interaction energy.
Therefore, a virtual photon can interact with elementary particles' electric charges. Being virtual, this photon is deep in the potential well and provides an electrostatic interaction.
It was shown in the article
| [22] | Petro O. Kondratenko. Structure of the Atomic Nuclei in the Universe Model with Minimal Initial Entropy // Physical Science International Journal, ISSN: 2348-0130, 2016. Vol. 12, Issue: 3. P. 1-12. https://doi.org/10.9734/PSIJ/2016/28694 |
[22]
that it is possible to describe the Coulomb interaction using virtual photons only by assuming that circularly polarized photons provide such an interaction. This fact is facilitated by the presence of electron helicity
. At the same time, the helicity of electrons is negative, i.e., they are left-polarized, and positrons are positive - right-polarized. Therefore, it can be assumed that a negative charge will absorb a left-polarized circular electromagnetic wave and a positive one - a right-polarized one. At the same time, they will emit a wave of a different polarization.
A right-polarized wave emitted by a negative charge is described by the sum of two linearly polarized waves:
(8)
Of course, an electromagnetic wave must be described by a formula
however, for clarity, the representation of waves by trigonometric functions is used here.
The distance between the charges will be equal to λ/2. The Ez wave resembles a standing wave in a pipe; the reverse wave occurs without losing phase. As for the Ey wave, it resembles a standing wave in a string. In this case, the return wave loses its phase by a factor of π. As a result, the wave reflected from the positive charge will become left-polarized. As a result, an interaction will be established between these charges, which ensures attraction between them. If the charges had the same sign, the absorption of waves by the above mechanism would not occur. There would be repulsion between them.
It is worth detailing the interaction between the charges a little. In nature, everything happens according to the Laws of unity and similarity
| [7] | Petro O. Kondratenko. Model of the Creation and Evolution of the Universe with Minimal Initial Entropy. Fundamental Interactions in the Universe / LAMBERT Academic Publishing. - 2017. – 130 p. https://kondratenko.com.ua |
| [17] | Nakamura, K (2010). "Review of Particle Physics". Journal of Physics G: Nuclear and Particle Physics. 37(7A): 075021. Bibcode: 2010JPhG... 37g5021N. https://doi.org/10.1088/0954-3899/37/7A/075021 |
[7, 17]
. Therefore, the Law of Similarity also exists for fundamental interactions. Therefore, we will use the strong interaction mechanism to explain the electromagnetic and gravitational interaction.
The formula determines the energy of the electrostatic charge field
The emission of a virtual photon by the field of a charge can lower the energy of the electrostatic field of this charge since this energy depends not only on the size of the charge but also on the particle's mass. However, the charge of the particle is quantized, i.e., constant. Therefore, the emission of a virtual photon is carried out by the electric field of the particle's charge due to the energy of the Scalar Field localized on the same particle and responsible for its mass. The transfer of a virtual photon between particles is accompanied by the reverse transfer of energy of the Scalar Field, which restores the energy of the Scalar Field of the first charge. The absorption of a virtual photon by a charge of the opposite sign leads to the transfer of the energy of the virtual photon to it and the restoration of the energy of the electrostatic field. Therefore, the Scalar Field is localized on it. Thus, the binding energy between charges of opposite signs will equal twice the energy of a virtual photon. The absorption of a photon is a dynamic process. Therefore, it is immediately accompanied by the emission of another virtual photon with the opposite polarization, which can be perceived as the appearance of a standing electromagnetic wave. The interaction occurs between the charges, but the Scalar Field controls it, i.e., the Scalar Field, in this case, acts as a calibration field.
When charges of the same name interact, there is no condition for the absorption of a virtual photon directly by the charge. Additional energy transfer of the Scalar Field to the charge is required to detect such an interaction. As a result, this leads to an increase in the energy of the system of two charges of the same name due to the Scalar Field. There is repulsion between the charges.
Thus, we have interconnected electric and magnetic fields and free and virtual photons. All of them are in three-dimensional space, providing electromagnetic interaction between electrically charged particles using the control of the Scalar Field as a catalyst for the process.
2.4. Charges of Gravitational Interactions
Let's look at the gravitational interaction between an electron and a proton
J(10)
The ratio between gravitational and electrostatic interactions in this pair of particles is 4.4126-40. It is worth paying attention to one more relationship between gravitational and electrostatic interactions in a pair of Planck particles, since time, mass and Planck length determine the birth of the Universe
0.2304·10-27:1.23·10-27.(11)
As we can see, the electrostatic and gravitational interactions now have the same order of magnitude. We obtain such a ratio under the assumption that the value of ε0 is the same in all layers of the layered space.
There is a relatively strong electric field above the Earth's surface. The Earth has a relatively large electric charge
, the value of which is approximately equal to 5·10
5 C. At the same time, almost the entire electric field is localized between the Earth's surface and the ionosphere. The solar wind (stochastic solar flares) supplies charges to the ionosphere, stabilizing the magnitude of the electric field to a certain extent. At the same time, the intensity of cosmic radiation has a time-varying, non-periodic character. A similar assumption will be valid for the Sun. In this case, the question arises: Why does the electrostatic interaction between the Sun and the Earth not affect the characteristics of the Earth's orbit around the Sun?
The reason is that electromagnetic interaction is realized exclusively in our three-dimensional space. If all the charged particles stood still, there would be conditions for creating a standing wave for an arbitrary distance between the charges. However, all charges are moving. Therefore, at large distances, such as between the Sun and the planets, the condition for the emergence of a standing wave will be violated. Hence, electric charges are not influenced by the parameters of Earth's motion. What is different about the gravitational interaction is that it manifests itself at an arbitrary distance between objects.
Gravitational interaction fully manifests in the Universe, regardless of the constant movement of stars, galaxies, and their clusters. In addition, experience shows that the transformation of a star into a black hole does not lead to the disappearance of the gravitational attraction of stars to the black hole. It exists and ensures that matter from near space is captured by a black hole, including stars and other black holes that have come close enough to the black hole. A multi-dimensional Scalar Field can only provide the presence of gravitational interaction and the release of matter and energy beyond the boundaries of a black hole
.
The Scalar Field "knows" the coordinates of all masses in the Universe, using its multidimensionality and the presence of information interaction between the layers of stratified space, which occurs through a delocalized point
. Therefore, it can always organize interaction between massive bodies or massive systems of bodies (galaxies). It is clear that not only the Scalar Field but also the gravitational field generated by it, including gravitational waves, must have a dimension that exceeds the dimension of our Universe.
Unlike electromagnetic interaction, gravitational interaction causes attraction between masses of the same sign. Therefore, the gravitational wave should have the form of a double spiral, the wavelength of which is equal to the distance between the interacting masses. Since the Scalar Field, thanks to its dimension, can instantly overcome arbitrary distances in the Universe, it can contribute to the fact that the interaction between galaxies will occur almost instantly.
At all hierarchical levels, gravitational interaction occurs due to virtual gravitational waves (gravitons) exchange. This exchange looks like this. Under the influence of the Scalar Field, one mass emits a graviton (gravitational wave) in the direction of the second mass. At the same time, the energy of this body decreases. The movement of the graviton to the second mass causes the opposite simultaneous movement of the Scalar Field responsible for the second mass. By absorbing the graviton, the second mass returns the lost energy. The dynamics of graviton capture causes a new graviton to be emitted by the second mass. The cycle of graviton emissions and absorptions repeats itself endlessly. Therefore, the Scalar Field also acts as a calibration field of interaction in this case.
Let's pay attention to the fact that Newton's formula for gravitational interaction provides an invariant value when the scale of interaction changes. For this, it is necessary to simultaneously reduce the values of the interacting masses and the distance between them by the same number of times. The gravitational interaction at different hierarchical levels uses this fact. Since the graviton wave is multi-dimensional, it immediately takes advantage of a delocalized point of interaction between the three-dimensional and two-dimensional worlds. Using its multidimensionality, the Scalar Field can always organize interaction between massive bodies (planets, stars) or massive systems of bodies (galaxies, clusters of galaxies).
To model the gravitational interaction at different hierarchical levels, we will take some numbers as a basis, which can be refined in the future according to the data of observation of the Universe. First of all, let's pay attention to the estimate of the radius of the Universe and the mass of matter in the Universe given in
| [7] | Petro O. Kondratenko. Model of the Creation and Evolution of the Universe with Minimal Initial Entropy. Fundamental Interactions in the Universe / LAMBERT Academic Publishing. - 2017. – 130 p. https://kondratenko.com.ua |
[7]
:
RU = 1.3·10
26 m,
MU = 4.18·10
51 kg. The effective value of the number of stars with a mass equal to the mass of the Sun is N
ef21. This quantity can be imagined as the product of the total number of galaxies (N
tng) by the number of stars (N
Star) in the galaxy: N
ef = N
tng·N
Star. Assume that N
tng = N
Star10, which corresponds to the estimate given in the article
. Let us further assume that the total number of galaxies in the Universe is divided between the number of galaxy clusters (N
gc) and the number of galaxies in the cluster (N
g), so that N
g = 2·10
3 galaxies, and N
gc = 2.3·10
7.
And, finally, we will introduce the scaling factor (k) for all HLs where the gravitational interaction is manifested. The value of the scaling factor k must be different for different HLs.
Above, we talked about temporal unity on different HLs. From here it is easy to calculate the value of k. In the Universe Δt = h/Mminc2. In another layer Δt1 = h/kMminc2.
At the same time
From here
The calculation of the values of the parameters included in Newton's formula for each hierarchical level is given in
Table 2.
Table 2. Calculation of gravitational interaction parameters at different hierarchical levels.
ІР | RІР, м | RIPmin, м | Mmin, кг | RІР/RIPmin | k | kMmin | k·RIPmin | k·RIP |
Planetary systems | ~4.5·1012 | 6.4·106 | 6·1024 | 0.7·106 | 2.3·10-37 | 1.4·10-12 | 1.5·10-30 | 1.1·10-24 |
Star systems | ~4.7·1020 | ~4.5·1012 | 2·1030 | 1.04·108 | 5·10-44 | 1·10-12 | 2.3·10-30 | 2.3·10-22 |
Cluster of galaxies | ~2·1023 | ~4.7·1020 | 9·1040 | 425 | 2.3·10-52 | 2.1·10-11 | 1.1·10-31 | 7·10-29 |
Metagalaxy (between galaxy clusters) | 1.3·1026 | ~2·1023 | 1.8·1044 | 650 | 2.5·10-55 | 2.2·10-14 | 5·10-32 | 3.3·10-29 |
To interpret the obtained results, let's pay attention to the fact that the average distance between quarks in two-dimensional is 10
-13 m, and between dyons in one-dimensional world - 6·10
-34 m
. A comparison of the parameters given in the last three columns of
Table 2 with the parameters of particles in the three layers of the stratified Super-Universe shows that the reduced distances are significantly smaller than in a two-dimensional world but larger than in a one-dimensional one. At the same time, the minimum reduced mass is several orders of magnitude smaller than the Planck mass and several orders of magnitude larger than the mass of particles in two-dimensional and three-dimensional worlds. Such a result may indicate that gravitational waves propagate simultaneously in three layers of the stratified Super-Universe. Therefore, in theory, we deal with reduced masses and distances that describe the gravitational interaction in the multi-dimensional Super-Universe.
Let us pay attention to one more fact: the last three columns of
Table 2 show that the reduced mass and distance parameters for star systems (galaxies) have extreme values. So, these masses are closer to three-dimensional space. From here, we can draw another conclusion: the parameter G in Newton's formula should be more significant for interactions in galaxies than in planetary systems, while between galaxies is smaller than for planetary systems, and between galaxy clusters is even smaller.
The charges of gravitational interactions on various HLs of the Universe are the reduced masses kM
min, presented in
Table 2. For planetary and stellar HLs, the magnitudes of gravitational charges have one order of magnitude. In the case of galaxy clusters, the magnitude of the gravitational charge is an order of magnitude greater.
We saw that the magnitude of the gravitational interaction between galaxy clusters decreases, which purely phenomenologically can be imagined as an additive repulsion, the magnitude of which increases with increasing distance. In this case, we will get an accelerated scattering of galaxies. The multidimensionality of the Scalar Field and gravitational waves will be responsible for the fragile gravitational interaction between bodies.
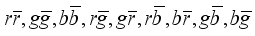 . The charges of gluons, which are in the field of reduced symmetry, are given here. The symmetry of the free gluon is described in terms of the SU (3) group.
. The charges of gluons, which are in the field of reduced symmetry, are given here. The symmetry of the free gluon is described in terms of the SU (3) group. 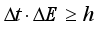 (2)
(2) 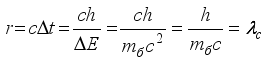 (3)
(3) 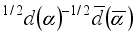 ] or [
] or [ 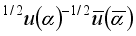 ], where α = r, g, b. Therefore, the power of SF quarks will be generated from vacuum particles under conditions of reduced symmetry, with only a neutral quark-antiquark pair corresponding to a neutral pion in the Universe. If this pair was born in the triplet of quarks, which are the constituents of a neutron, then it should have a quark structure
], where α = r, g, b. Therefore, the power of SF quarks will be generated from vacuum particles under conditions of reduced symmetry, with only a neutral quark-antiquark pair corresponding to a neutral pion in the Universe. If this pair was born in the triplet of quarks, which are the constituents of a neutron, then it should have a quark structure 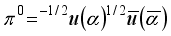 and the constituents of a proton -
and the constituents of a proton - 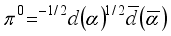 .
. 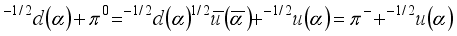 (4)
(4) 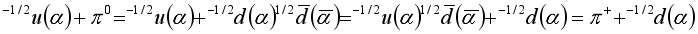 (5)
(5) 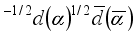 and
and 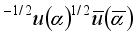 . In the field of a group of quarks that make up a proton and a neutron, the polarization of these pairs and the exchange of quarks in their structures take place:
. In the field of a group of quarks that make up a proton and a neutron, the polarization of these pairs and the exchange of quarks in their structures take place: 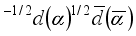 +
+ 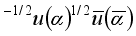
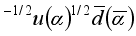 +
+ 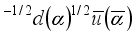 ,(7)
,(7)